前面，我们假设可以投资的一种股票及一种国库券，而国库券没有风险，所以投资考虑就集中在那个有风险的股票上。现在我们把问题的复杂都及真实度增加一点，考虑有两个股票可供选择。如果我们不投资国库券，只在这两个股票之间进行资产配置，那么我们会有什么样的风险收益曲线呢？

图表 44 包含两只股票的投资组合的风险收益

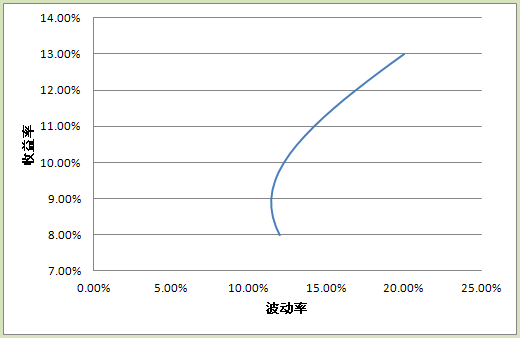
我们知道，不同的公司虽然独立经营，但任何两个公司的业绩都会受到宏观经济的影响，任何两个股票也同时受市场的总体投资情绪影响，因此两个股票之间应该有一定的相关性。我们假设现在这两个股票具有一些正的相关性，就是说要涨大家一起张，要跌大家也一起跌，只是幅度有所区别。在这种情况下，我们会得到包含两个股票的投资组合的风险收益曲线。比较奇妙的是，随着期望收益率的上升，波动率先会下降，然后再上升。我们显然不会选择曲线的下半部分，因为同样的波动率下，我们会选择具备更高收益率的上半部分。

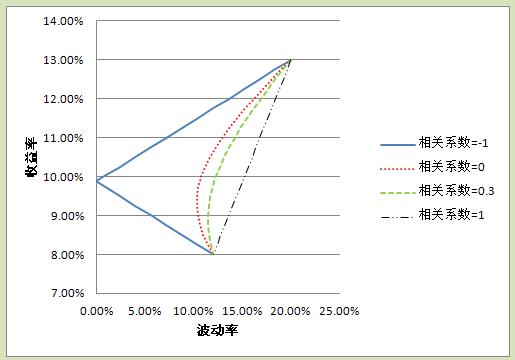
如果我们调整这两个股票之间相关性，比方说，两个股票之间完全的负相关，就是说一个股票上涨，那么另一个股票就会下跌，那么这两个股票所构成的组合的风险收益曲线就会如同图表 46 中的折线，如果两个股票完全的正相关，那么投资组合的曲线就如同 图表 46 中的直线，如果两个股票之间的相关性在负1到正1之间，那么曲线就同 图表 46 中的曲线。

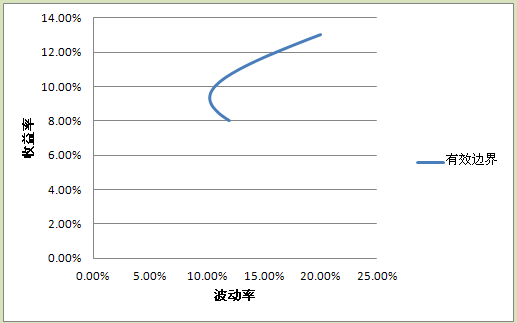
假如可供我们投资的股票范围涵盖市场上的所有股票，那么对应不同的投资组合，就会得到无数条风险收益曲线，我们把这些风险收益曲线的最外面的边界勾勒成一条曲线，就得到了一条有效率的边界。有效率的含义是，我们只会选择边界点所对应的资产配置比例，来分配在不同股票之间的投资比例，因为位于有效边界下方的点，具有同样的波动率，却具有更低的收益率。

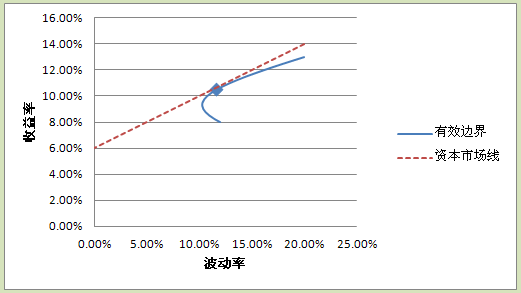
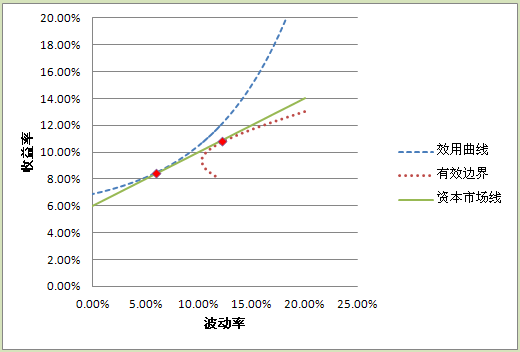
如果除了股票，我们还能够投资具有6%固定年收益率的债券，那么我们就得到一条新的直线，这条直线的端点所对应的资产配置是把所有的钱都用来买债券，直线与有效边界具有一个切点，这个切点对应的资产配置是把全部的钱都用来买股票。这个切点还有一个十分特别的含义，假设我们是市场上的“一般人”，也就是说我们的资产配置比例等于全部市场参与者的平均水平，那么我们的资产在不同股票之间的资产比例，必然等于全部股票的市值的比例，否则我们就无法成为一个“一般人”了。如果我们是一个一般人，那么我们可以把这条直线称为资本市场线。这条直线，就是全体投资者所面临的平均的风险收益曲线。

图表 45 不同相关性股票构成的投资组合的风险收益

图表 46 很多股票所形成的有效率边界

图表 47 债券和股票组合所形成的资本市场线

与前面类似，我们把全体投资者看作一个人，画出这个特别的人的效用曲线，就得到了我们的资产在股票和债券之间的配置比例。

很明显，假定股票市场只有一个买家，及两个资产：一种股票及一个国库券，是非常脱离现实的。但是图47给了我们一个清楚的暗示，金融分析可以非常理性，经济学的重要分析工具：预算线及无差异曲线，可以用在金融决策上。科学的突破都是来自类比。植物与动物有共同性与差异性。人与猴子也有共同性与差异性。图47是观念的大突破。想到这个思路的人，耶鲁大学托宾教授因此拿到经济学诺贝尔奖。

我们已经知道国债的无风险收益率，也知道每个股票的预期收益率、整个股票市场的平均预期收益率，同时也知道每个股票的波动率，以及整个股票市场的平均波动率，我们可以构造一个新的符号，叫做β，称为贝塔。

贝塔 = （某个股票的预期收益率 – 无风险收益率）/（整个市场的预期收益率 – 无风险收益率）

我们也可以把上面的公式换一种形式：

某个股票的预期收益率 =无风险收益率 + 这个股票的贝塔×（整个市场的预期收益率 – 无风险收益率）

 图表 48资本市场线与效用曲线

上面的这个公式就称为资产定价模型，是近一百年来全世界金融研究中最顶级的成果之一，提出贝塔这个概念，及分析模型的夏普先生后来获得了诺贝尔经济学奖。贝塔概念简单到任何商学硕士(MBA)都可以学会，用在实际投资决策上。

亲爱的读者，你们在股市投了大量的资金，你们没有听过贝塔？老天，你们是用自己的钞票点火取暖。